k-Means and Voronoi Tesselation: Built with Processing
This is a small animation of how one of the best known cluster algorithm - the k-Means - works, and how it is related to the voronoi tesselation.
Click on the image above to see the applet (requires Java and may take some time to load).
The aim of clustering analysis is to group data in such a way that similar objects are in one cluster and objects of different clusters are disimilar. The k-Means algorithm basically consists of three steps:
- an initial set of 'k' (where 'k' is the number of clusters) so-called centroids,
i.e. virtual points in the data space is randomly created, - every point of the data set is assigned to its nearest centroid and
- the position of the centroid is updated by the means of the data points assigned to that cluster. In other words, the centroid is moved toward the
center of its assigned points.
This is done until no centroid was shifted in one iteration resulting in 'k' subsets/cluster.
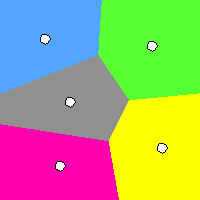
The assignment of points to centroids results in a partitioning of the data space. It results in virtual borders between each two centroids, where the distance is equal on each side of the border to these centroids. This kind of partitioning is also known as a Voronoi tesselation.
In this small animation a grid of points is created with each pixel as one point and 'k' randomly created centroids then the k-Means runs until convergence. After convergence the centroids are again randomly initialized and the k-Means runs again and so on. Since every possible point of the input space is assigned to one centroid the result is a Voronoi tesselation of the input space.
@author Fabian Dill, University of Konstanz
@created 27 November 2005
Source code: kMeansVoronoi
Built with Processing
vielen dank für das teilen
vielen dank für das teilen des algorithmus!
wir sind architekturstudenten und wollen den lloyd's algorithmus verwenden um unser zu beplanendes grundstück in fünf gleich grosse voronoi zellen zu teilen.
mit linien gezeichnet sind es wie folgt aus:
line(20, 20, 76, 40);
line(76, 40, 176, 76);
line(176, 76, 240, 112);
line(240, 112, 124, 280);
line(124, 280, 106, 268);
line(106, 268, 20, 104);
line(20, 104, 20, 20);
allerdings fehlt uns das wissen, wie wir diesen bereich für den lloyd's algorithm definieren. hat vielleicht jemand einen TIPP wie wir das anstellen könnten?
besten dank!
david
Post new comment